Parametarsko zadavanje

☰ matematika1

Implicitno zadavanje Načini zadavanja funkcija Klasifikacija funkcija

Parametarsko zadavanje

Funkcija se zadaje parametarski tako da se i zadaju kao funkcije parametra ,

$\displaystyle x$	$\displaystyle =\varphi (t)$
$\displaystyle y$	$\displaystyle =\psi(t), \qquad t\in \mathcal{T}\subseteq \mathbb{R}.$

Graf parametarski zadane funkcije je krivulja u ravini, $\Gamma\subset \mathbb{R}^2$ , definirana s

$\displaystyle \Gamma=\{(x,y): x=\varphi (t),\ y= \psi(t), \ t\in \mathcal{T}\}.$

(4.2)

Kao i kod implicitno zadanih funkcije, kod parametarski zadane funkcije jednoj vrijednosti varijable

može odgovarati više vrijednosti varijable

Na primjer, parametarska jednadžba kružnice iz primjera 4.1 glase

$\displaystyle x$	$\displaystyle =2\sin t$
$\displaystyle y$	$\displaystyle =1+2\cos t, \qquad t\in [0,2\pi].$

Lako se provjeri da

zadovoljavaju jednadžbu kružnice iz primjera 4.1. Uočljivo je da je ovo samo jedna od beskonačno mogućih parametarskih jednadžbi ove kružnice (navedite još barem jednu).

Primjer 4.3 Cikloida je krivulja koju opisuje fiksna točka kružnice kada se ta kružnica kotrlja bez klizanja po pravcu. Parametarska jednadžba cikloide glasi (slika 4.7)

$\displaystyle x$	$\displaystyle =r(t-\sin t)$
$\displaystyle y$	$\displaystyle =r(1-\cos t), \qquad t\in \mathbb{R}.$

**Slika 4.7:** Cikloida
$\begin{figure}\begin{center} \epsfig{file=slike/ciklo.eps,width=9.6cm} \end{center}\end{figure}$

Zadatak 4.2

(a)

Epicikloida je krivulja koju opisuje točka na kružnici kada se ta kružnica bez klizanja kotrlja po vanjskom rubu druge kružnice. Hipocikloida je krivulja koju opisuje točka na kružnici kada se ta kružnica bez klizanja kotrlja po unutrašnjem rubu druge kružnice. Nađite jednadžbe epicikloide i hipocikloide u matematičkom priručniku i nacrtajte te krivulje pomoću programa NetPlot .

(b)

Izvedite implicitnu jednadžbu cikloide:

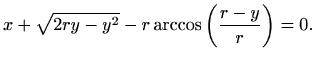
$\displaystyle x+\sqrt{2ry-y^2}-r \arccos \bigg( \frac{r-y}{r} \bigg)=0.$

(c)

Kako glasi jednadžba cikloide koja polazi iz točke

? Provjerite rješenje pomoću programa NetPlot .

Primjer 4.4 Izvedimo parametarsku jednadžbu Descartesovog lista iz primjera 4.2. Iz jednadžbe

$\displaystyle x^3+y^3-3xy=0$

vidimo da krivulja prolazi kroz točku

. Ako je $x,y\neq 0$ , tada jednadžbu možemo podijeliti s

što daje

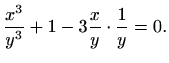
$\displaystyle \frac{x^3}{y^3}+1-3\frac{x}{y}\cdot \frac{1}{y}=0.$

Uvedimo novu varijablu

$\displaystyle t=\frac{x}{y}$

što daje

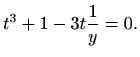
$\displaystyle t^3+1-3t\frac{1}{y}=0.$

Dakle,

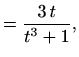$\displaystyle y$	$\displaystyle =\frac{3\,t}{t^3+1},$
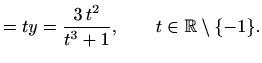$\displaystyle x$	$\displaystyle =ty=\frac{3\,t^2}{t^3+1}, \qquad t\in\mathbb{R}\setminus\{-1\}.$

Zadatak 4.3 Koje dijelove Descartesovog lista na slici 4.6 dobijemo kada parametar

poprima vrijednosti u intervalima $(-\infty,-1)$ ,

i $[1,\infty)$ ? Kod rješavanja zadatka možete koristiti program NetPlot .

U ovoj i sljedećoj glavi vidjet ćemo da su najbolje razvijeni teoretski rezultati za analiziranje eksplicitno zadanih funkcija, dok se implicitno i parametarski zadane funkcije analiziraju pomoću odgovarajućih prilagodbi tih rezultata. Stoga je kod ispitivanja parametarski zadanih funkcija važno znati kada je i na kojem području s i eksplicitno zadana funkcija ili . Pri tome je važno uočiti da su kod parametarski zadanih funkcija varijable i ravnopravne. Sljedeći teorem nam daje uvjete za postojanje funkcije , dok se analogni teorem za slučaj funkcije dobije zamjenom varijabli.

Teorem 4.1 Neka je skup $\Gamma$ definiran relacijom (4.2) graf neke parametarski zadane funkcije. Ako je funkcija $\varphi$ injekcija, tada je $\Gamma$ ujedno i graf eksplicitno zadane funkcije

pri čemu je $f=\psi \circ \varphi ^{-1}$ .

Dokaz.

Neka je skup $\mathcal{D}= \varphi (\mathcal{T})$ slika funkcije $\varphi$ . Kako je $\varphi$ injekcija, a ujedno i surjekcija sa skupa $\mathcal{T}$ na skup $\mathcal{D}$ , zaključujemo da je $\varphi$ bijekcija između skupova $\mathcal{T}$ i $\mathcal{D}$ . Po Teoremu o inverznoj funkciji 1.1 postoji inverzna funkcija $\varphi ^{-1}:\mathcal{D}\to \mathcal{T}$ . Definirajmo kompoziciju $f=\psi \circ \varphi ^{-1}$ . Očito vrijedi $f:\mathcal{D}\to \mathbb{R}$ . Nadalje,

$\displaystyle y=\psi(t)=\psi(\varphi ^{-1}(\varphi (t)))=\psi(\varphi ^{-1}(x))=f(x),$

i teorem je dokazan.

Q.E.D.

Implicitno zadavanje Načini zadavanja funkcija Klasifikacija funkcija