☰
matematika1
Lokalni ekstremi i intervali
DERIVACIJE I PRIMJENE
Točke infleksije i intervali
Točke infleksije
Odredite
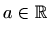 takav da funkcija
takav da funkcija  zadana s
zadana s
ima točku infleksije u 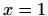 , a zatim odredite sve točke infleksije funkcije
, a zatim odredite sve točke infleksije funkcije  .
.
Rješenje. Izračunajmo drugu derivaciju funkcije  . Vrijedi
. Vrijedi
pa je
Prema
![[*]](../icons.gif/crossref.gif) [M1, teorem 5.16], nužan uvjet da funkcija
[M1, teorem 5.16], nužan uvjet da funkcija  ima točku infleksije u
ima točku infleksije u 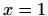 je
je 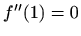 , odnosno
, odnosno
Ova jednadžba ima dva rješenja 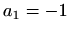 i
i 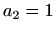 . Za
. Za 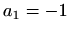 dobivamo funkciju
dobivamo funkciju
koja nema točaka infleksije. Za 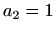 dobivamo funkciju
dobivamo funkciju
Njena druga derivacija je
Rješenja jednadžbe 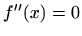 su
su
Izračunajmo još vrijednost treće derivacije u dobivenim točkama. Vrijedi
Uvrštavanjem vidimo da je
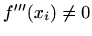 za
za 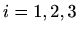 pa, prema
pa, prema
![[*]](../icons.gif/crossref.gif) [M1, teorem 5.18], funkcija
[M1, teorem 5.18], funkcija  ima točke infleksije u
ima točke infleksije u 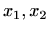 i
i
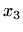 i traženi parametar je
i traženi parametar je 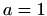 .
.
Lokalni ekstremi i intervali
DERIVACIJE I PRIMJENE
Točke infleksije i intervali
![]() takav da funkcija
takav da funkcija ![]() zadana s
zadana s
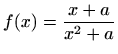
![]() . Vrijedi
. Vrijedi
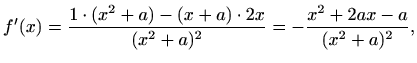
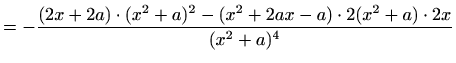
![$\displaystyle =-\frac{2\,[(x+a)\cdot(x^2+a)-(x^2+2ax-a)\cdot2x]}{(x^2+a)^3}$](img2364.gif)
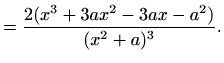
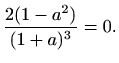
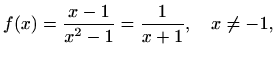
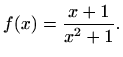
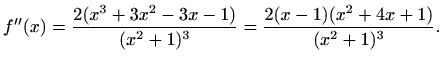
![$\displaystyle =\frac{2\,[(3x^2+6x-3)(x^2+1)^3-(x^3+3x^2-3x-1)\cdot3(x^2+1)^2\cdot2x]}{(x^2+1)^6}$](img2375.gif)
![$\displaystyle =\frac{6\,[(x^2+2x-1)(x^2+1)-(x^3+3x^2-3x-1)\cdot2x]}{(x^2+1)^4}.$](img2376.gif)