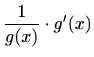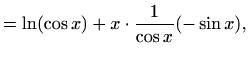☰
matematika1
Deriviranje kompozicije funkcija
DERIVACIJE I PRIMJENE
Deriviranje implicitno zadane funkcije
Logaritamsko deriviranje
Odredite derivaciju funkcije  zadane s:
zadane s:
- a)
-
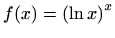 ,
,
- b)
-
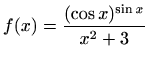 ,
,
- c)
-
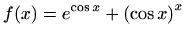 .
.
Rješenje. Derivacije zadanih funkcija računamo postupkom logaritamskog deriviranja iz
![[*]](../icons.gif/crossref.gif) [M1, poglavlje 5.1.6].
[M1, poglavlje 5.1.6].
- a)
- Iz svojstava logaritamske funkcije slijedi
odakle deriviranjem dobivamo
Sada je
- b)
- Zbog svojstava logaritamske funkcije je
Deriviranjem prethodne jednakosti dobivamo
Sada je
- c)
- Vrijedi
Budući je
dovoljno je logaritamski derivirati funkciju
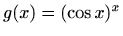 . Iz
. Iz
deriviranjem slijedi
Dakle,
Deriviranje kompozicije funkcija
DERIVACIJE I PRIMJENE
Deriviranje implicitno zadane funkcije
![]() zadane s:
zadane s:
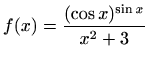 ,
,
![]() [M1, poglavlje 5.1.6].
[M1, poglavlje 5.1.6].
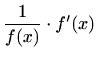
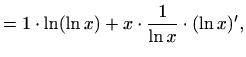
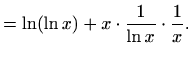
![$\displaystyle =f(x)\left[\ln (\ln x)+\frac{1}{\ln x}\right],$](img2103.gif)
![$\displaystyle =(\ln x)^x\left[\ln (\ln x)+\frac{1}{\ln x}\right].$](img2104.gif)
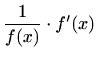
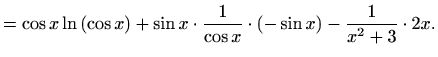
![$\displaystyle f'(x)=\frac{(\cos x)^{\sin x}}{x^2+3} \left[\cos x \ln(\cos x)-\frac{\sin^2 x}{\cos x}- \frac{2x}{x^2+3}\right].$](img2108.gif)