☰ matematika1

Cijeli brojevi OSNOVE MATEMATIKE Realni brojevi

Racionalni brojevi

U ovom poglavlju definirat ćemo skup racionalnih brojeva $\mathbb{Q}$ te dati osnovna svojstva tog skupa.

Na skupu

$\displaystyle % \mathbb{Z}\times \mathbb{N}=\{ (m,n): m\in \mathbb{Z},\ n\in \mathbb{N}\}$

definiramo relaciju $\sim$ s

$\displaystyle % (m_1,n_1)\sim(m_2,n_2) \Leftrightarrow m_1\cdot n_2=m_2\cdot n_1.$

$\sim$ je relacija ekvivalencije, na primjer $(2,3)\sim(4,6)\sim(6,9)$ .

Skup racionalnih brojeva $\mathbb{Q}$ je skup svih klasa ekvivalencije na skupu $\mathbb{Z}\times \mathbb{N}$ , odnosno

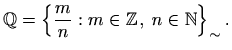
$\displaystyle % \mathbb{Q}=\left\{ \frac{m}{n}: m\in \mathbb{Z},\ n\in \mathbb{N}\right\}_{\sim}.$

Računske operacije , $\cdot$ i te relaciju potpunog uređaja $\leq$ na skupu $\mathbb{Q}$ definiramo redom kako slijedi:

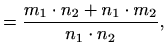$\displaystyle \frac{m_1}{n_1}+\frac{m_2}{n_2}$	$\displaystyle = \frac{m_1\cdot n_2+n_1\cdot m_2}{n_1\cdot n_2},$
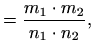$\displaystyle \frac{m_1}{n_1}\cdot \frac{m_2}{n_2}$	$\displaystyle = \frac{m_1\cdot m_2}{n_1\cdot n_2},$
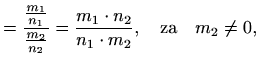$\displaystyle \frac{m_1}{n_1} : \frac{m_2}{n_2}$	$\displaystyle = \frac{\frac{m_1}{n_1}}{\frac{m_2}{n_2}}= \frac{m_1\cdot n_2}{n_1\cdot m_2}, \quad \textrm{za}\quad m_2\neq 0,$
$\displaystyle \frac{m_1}{n_1}\leq \frac{m_2}{n_2}$	$\displaystyle \Leftrightarrow m_1\cdot n_2\leq n_1\cdot m_2.$

Ovdje se zaista radi o definicijama, jer smo "nove" operacije i relaciju uređaja na lijevim stranama definirali pomoću poznatih operacija i uređaja na skupu $\mathbb{Z}$ na desnim stranama. Dakle, iste oznake za računske operacije i relaciju uređaja imaju različita značenja na lijevim i desnim stranama. Računske operacije i relacija uređaja na skupu $\mathbb{Q}$ su dobro definirane jer ne ovise o predstavniku klase ekvivalencije, na primjer $\frac{1}{3}+\frac{1}{4}=\frac{2}{6}+\frac{9}{12}$ . Za računske operacije vrijede poznata svojstva slično kao u teoremu 1.3.

Za razliku od skupova $\mathbb{N}$ i $\mathbb{Z}$ koji su diskretni, skup $\mathbb{Q}$ je gust, odnosno između svaka dva različita racionalna broja nalazi se beskonačno mnogo racionalnih brojeva.

Teorem 1.7 Skup $\mathbb{Q}$ je gust.

Dokaz.

Dovoljno je dokazati da se između svaka dva različita racionalna broja nalazi barem jedan racionalni broj. Neka je

$\displaystyle % q_1=\frac{m_1}{n_1},\quad q_2=\frac{m_2}{n_2} \quad \textrm{i} \quad q_1< q_2 \quad \textrm{odnosno}\quad m_1n_2<n_1m_2.$

Neka je

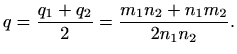
$\displaystyle % q=\frac{q_1+q_2}{2}=\frac{m_1n_2+n_1m_2}{2n_1n_2}.$

Tada je

jer je

. Slično vrijedi

i teorem je dokazan.

Q.E.D.

Unatoč tome što je $\mathbb{Q}$ gust, a $\mathbb{N}$ prebrojiv, oba skupa imaju jednako mnogo elemenata. Naime, skupovi $\mathbb{N}$ i $\mathbb{N}\times \mathbb{N}$ su ekvipotentni jer je funkcija $f:\mathbb{N}\to\mathbb{N}\times\mathbb{N}$ definirana s

$\begin{displaymath}% \begin{array}{ccccc} (1,1)_{f(1)}&(1,2)_{f(3)}&(1,3)_{f(6)}... ...)}&\cdots&&\\ (4,1)_{f(7)}&\cdots&&&\\ \cdots&&&& \end{array}\end{displaymath}$

bijekcija. Oznaka $(1,1)_{f(1)}$ znači

. Kako je $\mathbb{Z}$ ekvipotentan s $\mathbb{N}$ , to su i skupovi $\mathbb{N}$ i $\mathbb{Z}\times \mathbb{N}$ ekvipotentni. Konačno, iz $\mathbb{N}\subset \mathbb{Q}\subset \mathbb{Z}\times \mathbb{N}$ zaključujemo da je skup $\mathbb{Q}$ također ekvipotentan s $\mathbb{N}$ .

Cijeli brojevi OSNOVE MATEMATIKE Realni brojevi