![\begin{equation*}\begin{aligned}[t]
\quad x&\quad +&y&\quad -&z&\quad =&1, \\
2...
...z&\quad =&3, \\
x&\quad +&ay&\quad +&3z&\quad =&2.
\end{aligned}\end{equation*}](img643.gif)
![\begin{equation*}\begin{aligned}[t]
\lambda x&\quad +&y&\quad +&z&\quad =&1, \\ ...
...\
x&\quad +&y&\quad +&\lambda z&\quad =&\lambda^2.
\end{aligned}\end{equation*}](img644.gif)
![\begin{equation*}\begin{aligned}[t]
\quad x&\quad +&y&\quad -&z&\quad =&1, \\
2...
...z&\quad =&3, \\
x&\quad +&ay&\quad +&3z&\quad =&2.
\end{aligned}\end{equation*}](img643.gif)
![\begin{equation*}\begin{aligned}[t]
\lambda x&\quad +&y&\quad +&z&\quad =&1, \\ ...
...\
x&\quad +&y&\quad +&\lambda z&\quad =&\lambda^2.
\end{aligned}\end{equation*}](img644.gif)
Rješenje.
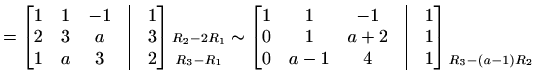 |
||
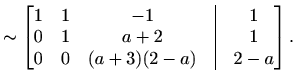 |
Slučaj 1. Promotrimo prvo slučaj kada je
![]() , odnosno kada
, odnosno kada
![]() . Tada možemo podijeliti treći redak s
. Tada možemo podijeliti treći redak s ![]() pa vrijedi
pa vrijedi
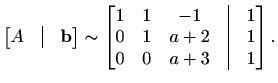
Budući je i
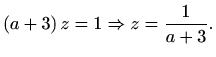
Uvrštavanjem u jednadžbu koja slijedi iz drugog retka, dobivamo
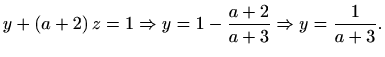
Sada iz prvog retka imamo
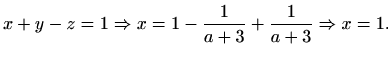
U ovom slučaju sustav ima jedinstveno rješenje koje glasi
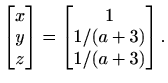
Slučaj 2. Ako je
Slučaj 3. Za ![]() je
je
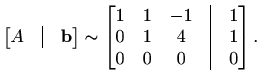
Sada iz drugog retka slijedi
a iz prvog je
Ako stavimo
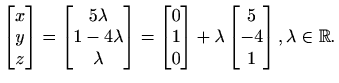
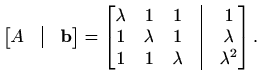
Da bi smanjili broj redaka koje treba pomnožiti s parametrom
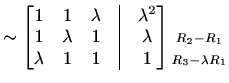 |
||
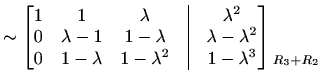 |
||
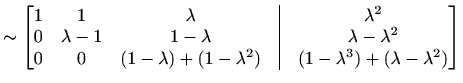 |
||
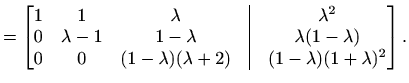 |
Slučaj 1. Ako je
![]() , odnosno
, odnosno
![]() , iz posljednje jednadžbe slijedi
, iz posljednje jednadžbe slijedi
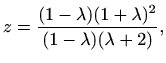 |
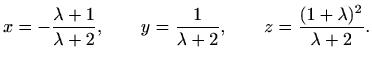 |