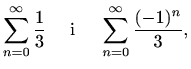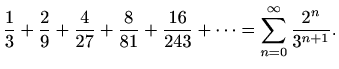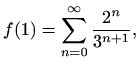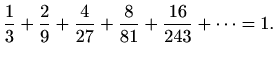☰
matematika1
Područje apsolutne konvergencije
NIZOVI I REDOVI
MacLaurinov razvoj racionalne funkcije
Taylorov razvoj racionalne funkcije
Razvijte u Taylorov red oko točke 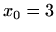 funkciju
funkciju  zadanu s
zadanu s
te odredite područje konvergencije dobivenog reda i izračunajte sumu reda
Rješenje. Odredimo prvo 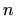 -tu derivaciju funkcije
-tu derivaciju funkcije  u točki
u točki 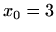 . Iz
. Iz
zaključujemo
pa je
Prema
![[*]](../icons.gif/crossref.gif) [M1, teorem 6.18], Taylorovog razvoj funkcije
[M1, teorem 6.18], Taylorovog razvoj funkcije  oko točke
oko točke 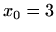 glasi
glasi
odakle uvrštavanjem 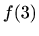 i
i
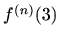 slijedi
slijedi
odnosno
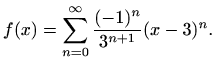 |
(6.10) |
Odredimo sada područje konvergencije dobivenog reda. Zbog
Cauchyjev kriterij povlači da red konvergira ako je 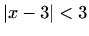 , odnosno za sve
, odnosno za sve
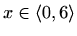 .
Redovi u točkama
.
Redovi u točkama 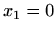 i
i 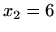 ,
,
divergiraju jer ne zadovoljavaju nužan uvjet konvergencije. Dakle, područje konvergencije je
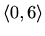 .
.
Izračunajmo sada sumu zadanog reda. Vrijedi
Za 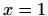 formula (6.10) daje
formula (6.10) daje
a jer je 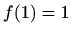 , slijedi
, slijedi
Područje apsolutne konvergencije
NIZOVI I REDOVI
MacLaurinov razvoj racionalne funkcije
![]() funkciju
funkciju ![]() zadanu s
zadanu s
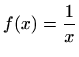
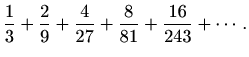
![]() -tu derivaciju funkcije
-tu derivaciju funkcije ![]() u točki
u točki ![]() . Iz
. Iz
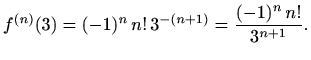
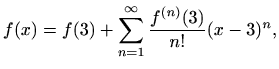
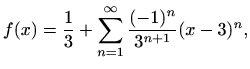
![$\displaystyle \lim_{n\to \infty} \sqrt[n]{\vert a_n\vert}=
\lim_{n\to \infty} \...
...\to \infty} \frac{\vert x-3\vert}{3^{\frac{n+1}{n}}} =\frac{\vert x-3\vert}{3},$](img3175.gif)