Ispitajte tok i skicirajte graf funkcije ![]() zadane s
zadane s
Rješenje. Prema postupku opisanom u
![]() [M1, poglavlje 5.9] ispitujemo sljedeće:
[M1, poglavlje 5.9] ispitujemo sljedeće:
Područje definicije zadane funkcije
je
![]() .
.
Funkcija ![]() nije ni parna ni neparna jer je
nije ni parna ni neparna jer je
Funkcija nije periodična jer je elementarna i ne sadrži neku od trigonometrijskih funkcija.
Rješavanjem jednadžbe ![]() dobivamo da su nul-točke
dobivamo da su nul-točke ![]() i
i ![]() .
.
Funkcija ![]() nema vertikalnih asimptota, jer je
nema vertikalnih asimptota, jer je
![]() .
.
Na lijevoj strani vrijedi
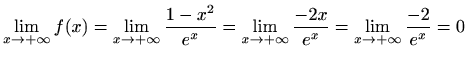 |
Na lijevoj strani primjenom L'Hospitalovog pravila dobivamo da je
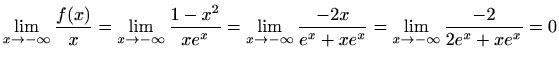
pa funkcija
Prva derivacija glasi
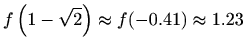 i
i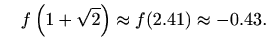
Iz predznaka prve derivacije slijedi da je
![]() strogo padajuća na intervalu
strogo padajuća na intervalu
![]() , dok je izvan njega strogo rastuća.
, dok je izvan njega strogo rastuća.
Iz predznaka druge derivacije slijedi da je
funkcija ![]() konveksna na
konveksna na
![]() , a inače konkavna.
, a inače konkavna.
Jednadžba
![]() se svodi na
se svodi na
![]() pa su njena rješenja
pa su njena rješenja
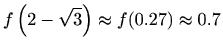 i
i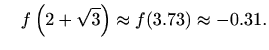
Graf funkcije je prikazan na slici 5.6.