- a)
-
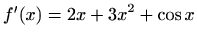 ,
,
- b)
-
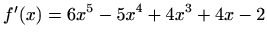 ,
,
- c)
-
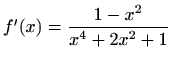 ,
,
- d)
-
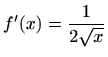 ,
,
- e)
-
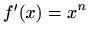 ,
,
- f)
-
![$ f'(x)=\displaystyle -\frac{\frac{1}{2\sqrt
x}+\frac{1}{6\sqrt[6]x}+\frac{1}{3\sqrt[3]{x^2}}}{\left(1+\sqrt[3]x\right)^2}$](img2660.gif) ,
,
- g)
-
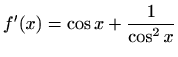 ,
,
- h)
-
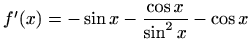 ,
,
- i)
-
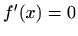 ,
,
- j)
-
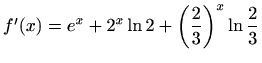 ,
,
- k)
-
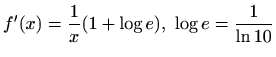 ,
,
- l)
-
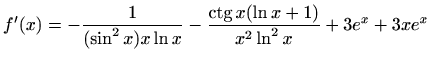 .
.
- a)
-
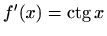 ,
,
- b)
-
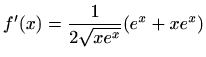 ,
,
- c)
-
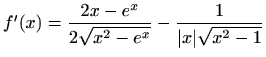 ,
,
- d)
-
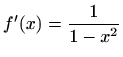 ,
,
- e)
-
![$ f'(x)=\frac{2x(x+\cos 2x)[\ln x+\cos
(2x+3)]-(x^2+\sin 2x)[1-2x\sin (2x+3)]}{x[\ln x+\cos (2x+3)]^2}$](img2671.gif) ,
,
- f)
-
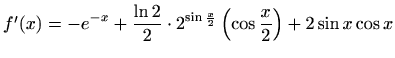 ,
,
- g)
-
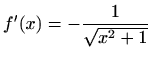 ,
,
- h)
-
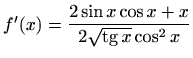 ,
,
- i)
-
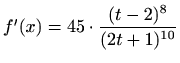 ,
,
- j)
-
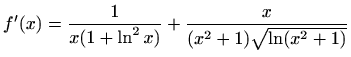 ,
,
- k)
-
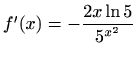 ,
,
- l)
-
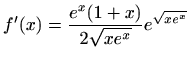 ,
,
- m)
-
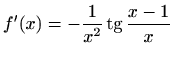 ,
,
- n)
-
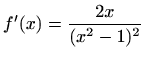 ,
,
- o)
-
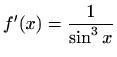 ,
,
- p)
-
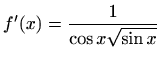 .
.
- a)
-
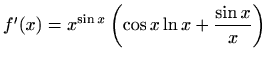 ,
,
- b)
-
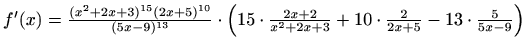 ,
,
- c)
-
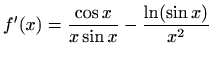 ,
,
- d)
-
![$ f'(x)=\displaystyle \frac{\sqrt
{(x-2)(x-4)}}{(x+1)(x+3)}\left[\frac{1}{2(x-2)}+\frac{1}{2(x-4)}-\frac{1}{x+1}-\frac{1}{x+3}\right]$](img2686.gif) ,
,
- e)
-
![$ f'(x)=\displaystyle \sqrt[x] x\cdot \frac{1-\ln x}{x^2}$](img2687.gif) .
.
- a)
-
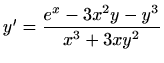 ,
,
- b)
-
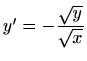 ,
,
- c)
-
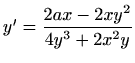 ,
,
- d)
-
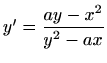 ,
,
- e)
-
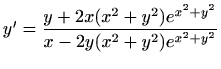 .
.
- a)
-
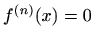 , za
, za 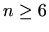 ,
,
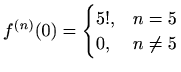 ,
,
- b)
-
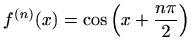 ,
,
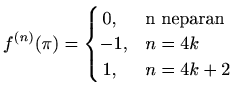 ,
,
- c)
-
![$ \displaystyle f^{(n)}(x)=(n-1)!4^n[(-1)^n(1+4x)^{-n} - (1-4x)^{-n}]$](img2698.gif) ,
,
![$ \displaystyle f^{(n)}(0)=(n-1)!4^n[(-1)^n-1]$](img2699.gif) .
.
- a)
-
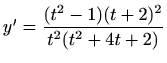 ,
,
- b)
-
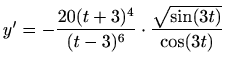 .
.
- a)
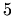 ,
,
- b)
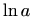 ,
,
- c)
-
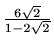 ,
,
- d)
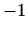 ,
,
- e)
- 0 ,
- f)
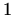 ,
,
- g)
- 0 ,
- h)
-
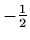 .
.
- a)
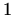 ,
,
- b)
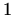 ,
,
- c)
-
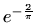 ,
,
- d)
-
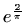 ,
,
- e)
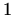 ,
,
- f)
-
![$ \frac{1}{\sqrt[6]{e}}$](img2721.gif) .
.
- a)
- Ekstremi:
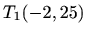 je lokalni maksimum,
je lokalni maksimum, 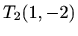 je lokalni minimum
je lokalni minimum
Intervali monotonosti:
 je rastuća na
je rastuća na
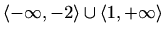 , padajuća na
, padajuća na
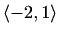
Intervali zakrivljenosti:
 je konkavna na
je konkavna na
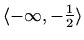 , konveksna na
, konveksna na
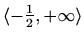
Točke infleksije:
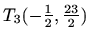
- b)
- Ekstremi:
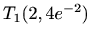 je lokalni maksimum,
je lokalni maksimum, 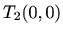 je lokalni minimum
je lokalni minimum
Intervali monotonosti:
 je padajuća na
je padajuća na
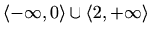 , rastuća na
, rastuća na
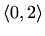
Intervali zakrivljenosti:
 je konveksna na
je konveksna na
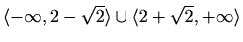 , konkavna na
, konkavna na
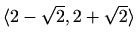
Točke infleksije:
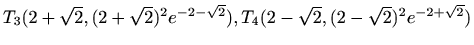
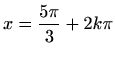 , lokalne maksimume u
, lokalne maksimume u
 i
i
 ,
,
- a)
- Najmanje otpadaka će biti za gredu kvadratnog presjeka sa stranicom
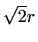 .
.
- b)
- Najveću nosivost će imati greda s dimenzijama poprečnog presjeka
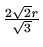 i
i
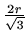 .
.
- a)
- Područje definicije:
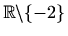
Parnost:
 nije ni parna ni neparna
nije ni parna ni neparna
Nul-točke:
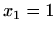
Asimptote:
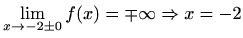 je
vertikalna asimptota
je
vertikalna asimptota
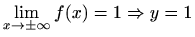 je
horizontalna asimptota
je
horizontalna asimptota
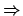 nema kosih asimptota
nema kosih asimptota
Ekstremi: nema
Intervali monotonosti:
 je svuda rastuća
je svuda rastuća
Točke infleksije: nema
Intervali zakrivljenosti:
 je
konveksna na
je
konveksna na
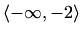 , konkavna na
, konkavna na
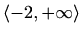
Graf funkcije: slika 5.9
- b)
- Područje definicije:
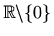
Parnost:
 nije ni parna ni neparna
nije ni parna ni neparna
Nul-točke:
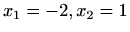
Asimptote:
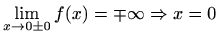 je
vertikalna asimptota
je
vertikalna asimptota
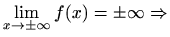 nema horizontalnih asimptota
nema horizontalnih asimptota
![$ \displaystyle\lim_{x\to \pm\infty}\frac{f(x)}{x}=1,\lim_{x\to
\pm\infty}[f(x)-x]=1\Rightarrow y=x+1$](img2766.gif) je kosa asimptota
je kosa asimptota
Ekstremi: nema
Intervali monotonosti:
 je svuda rastuća
je svuda rastuća
Točke infleksije: nema
Intervali zakrivljenosti:
 je
konveksna na
je
konveksna na
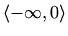 , konkavna na
, konkavna na
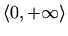
Graf funkcije: slika 5.10
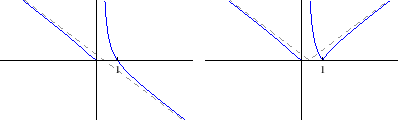
- c)
Područje definicije:
Parnost:
 je parna
je parna
Nul-točke:
Asimptote:
Područje definicije je
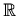 pa nema vertikalnih asimptota.
pa nema vertikalnih asimptota.
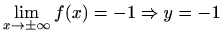 je
horizontalna asimptota
je
horizontalna asimptota
 nema kosih asimptota
nema kosih asimptota
Ekstremi:
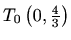 je
lokalni maksimum
je
lokalni maksimum
Intervali monotonosti:
 je rastuća na
je rastuća na
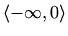 , padajuća na
, padajuća na
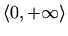
Točke infleksije:
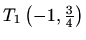 i
i
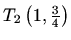
Intervali zakrivljenosti:
 je
konveksna na
je
konveksna na
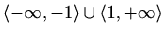 , konkavna na
, konkavna na
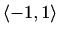
Graf funkcije: slika 5.11
- d)
Područje definicije:
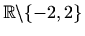
Parnost:
 je neparna
je neparna
Nul-točke:
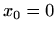
Asimptote:
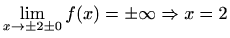 i
i
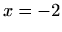 su vertikalne asimptote
su vertikalne asimptote
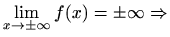 nema horizontalnih asimptota
nema horizontalnih asimptota
![$ \displaystyle\lim_{x\to \pm\infty}\frac{f(x)}{x}=2, \lim_{x\to
\pm\infty}[f(x)-2x]=0\Rightarrow y=2x$](img2776.gif) je kosa asimptota
je kosa asimptota
Ekstremi:
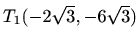 je lokalni maksimum,
je lokalni maksimum,
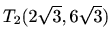 je lokalni minimum
je lokalni minimum
Intervali monotonosti:
 je rastuća na
je rastuća na
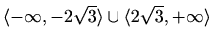 , padajuća na
, padajuća na
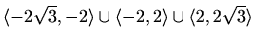
Točke infleksije:
Intervali zakrivljenosti:
 je konkavna na
je konkavna na
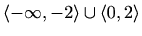 , konveksna na
, konveksna na
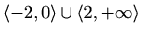
Graf funkcije: slika 5.12
- e)
Neka je
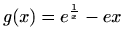 . Skicirajmo prvo graf funkcije
. Skicirajmo prvo graf funkcije 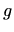 iz kojeg ćemo onda konstruirati graf funkcije
iz kojeg ćemo onda konstruirati graf funkcije  .
.
Područje definicije:
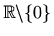
Parnost:
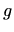 nije ni parna ni neparna
nije ni parna ni neparna
Nul-točke:
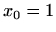
Asimptote:
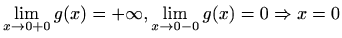 je desna vertikalna asimptota
je desna vertikalna asimptota
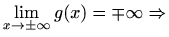 nema horizontalnih asimptota
nema horizontalnih asimptota
![$ \displaystyle\lim_{x\to
\pm\infty}\frac{g(x)}{x}=-e,\lim_{x\to \pm\infty}[g(x)+e
x]=1\Rightarrow y=-e x+1$](img2788.gif) je kosa asimptota
je kosa asimptota
Ekstremi: nema
Intervali monotonosti:
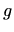 je svuda padajuća
je svuda padajuća
Točke infleksije: u
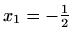 je točka infleksije
je točka infleksije
Intervali zakrivljenosti:
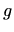 je
konveksna na
je
konveksna na
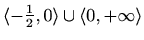 , konkavna na
, konkavna na
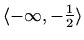
Graf funkcije: slika 5.13
- f)
Područje definicije:
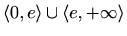
Parnost:
 nije ni parna ni neparna
nije ni parna ni neparna
Nul-točke:
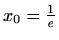
Asimptote:
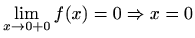 nije vertikalna
asimptota
nije vertikalna
asimptota
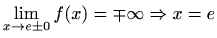 je
vertikalna asimptota
je
vertikalna asimptota
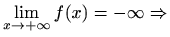 nema
horizontalnih asimptota
nema
horizontalnih asimptota
![$ \displaystyle\lim_{x\to +\infty}\frac{f(x)}{x}=-1,\lim_{x\to
+\infty}[f(x)+x]=-\infty\Rightarrow $](img2797.gif) nema kosih asimptota
nema kosih asimptota
Ekstremi: u
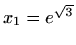 je lokalni
maksimum, u
je lokalni
maksimum, u
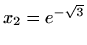 je lokalni minimum
je lokalni minimum
Intervali monotonosti:
 je rastuća na
je rastuća na
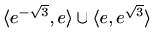 , padajuća na
, padajuća na
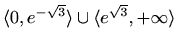
Točke infleksije:
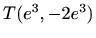
Intervali zakrivljenosti:
 je
konveksna na
je
konveksna na
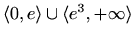 ,
konkavna na
,
konkavna na
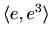
Graf funkcije: slika 5.14
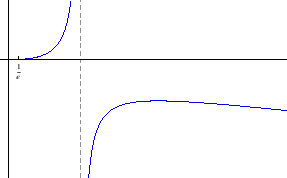
- a)
Područje definicije:
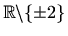
Parnost:
 je parna
je parna
Nul-točke: nema
Asimptote:
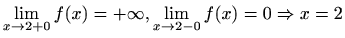 je desna vertikalna asimptota
je desna vertikalna asimptota
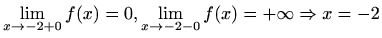 je lijeva vertikalna
asimptota
je lijeva vertikalna
asimptota
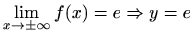 je
horizontalna asimptota, kosih asimptota nema
je
horizontalna asimptota, kosih asimptota nema
Ekstremi:
![$ T(0,\sqrt[4]{e})$](img2810.gif) je
lokalni maksimum
je
lokalni maksimum
Intervali monotonosti:
 je rastuća na
je rastuća na
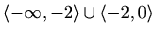 ,
padajuća na
,
padajuća na
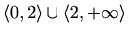
Graf funkcije: slika 5.15
- b)
Područje definicije:
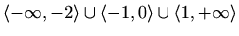
Parnost:
 nije ni parna ni neparna
nije ni parna ni neparna
Nul-točke: nema
Asimptote:
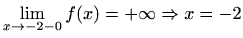 je lijeva
vertikalna asimptota
je lijeva
vertikalna asimptota
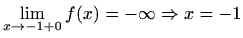 je desna
vertikalna asimptota
je desna
vertikalna asimptota
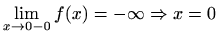 je lijeva
vertikalna asimptota
je lijeva
vertikalna asimptota
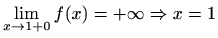 je desna
vertikalna asimptota
je desna
vertikalna asimptota
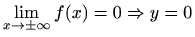 je
horizontalna asimptota
je
horizontalna asimptota
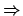 nema kosih asimptota
nema kosih asimptota
Ekstremi:
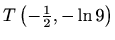 je lokalni maksimum
je lokalni maksimum
Intervali monotonosti:
 je rastuća na
je rastuća na
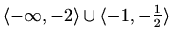 ,
padajuća na
,
padajuća na
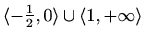
Graf funkcije: slika 5.16
- c)
Područje definicije:
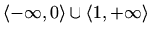
Parnost:
 nije ni parna ni neparna
nije ni parna ni neparna
Nul-točke: ne računamo
Asimptote:
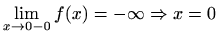 je lijeva
vertikalna asimptota
je lijeva
vertikalna asimptota
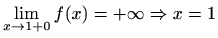 je desna
vertikalna asimptota
je desna
vertikalna asimptota
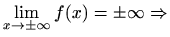 nema horizontalnih asimptota
nema horizontalnih asimptota
![$ \displaystyle\lim_{x\to \pm\infty}\frac{f(x)}{x}=1,\,\lim_{x\to
\pm\infty}[f(x)-x]=0\Rightarrow y=x$](img2825.gif) je kosa asimptota
je kosa asimptota
Ekstremi:
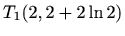 je lokalni minimum,
je lokalni minimum,
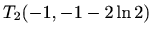 je lokalni
maksimum
je lokalni
maksimum
Intervali monotonosti:
 je rastuća na
je rastuća na
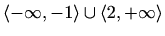 , padajuća na
, padajuća na
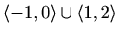
Graf funkcije: slika 5.17
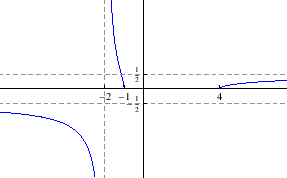
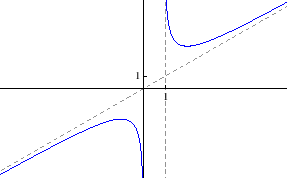
- d)
Područje definicije:
![$ \langle-\infty,-2\rangle\cup\langle-2,-1]\cup[4,+\infty\rangle$](img2831.gif)
Parnost:
 nije ni parna ni neparna
nije ni parna ni neparna
Nul-točke:
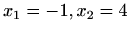
Asimptote:
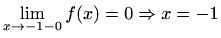 nije lijeva
vertikalna asimptota
nije lijeva
vertikalna asimptota
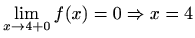 nije desna
vertikalna asimptota
nije desna
vertikalna asimptota
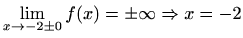 je
vertikalna asimptota
je
vertikalna asimptota
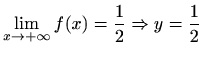 je desna horizontalna asimptota
je desna horizontalna asimptota
 nema desnu kosu asimptotu
nema desnu kosu asimptotu
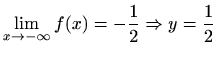 je lijeva horizontalna asimptota
je lijeva horizontalna asimptota
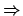 nema lijevu kosu asimptotu
nema lijevu kosu asimptotu
Ekstremi:
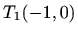 i
i 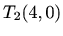 su lokalni
minimumi
su lokalni
minimumi
Intervali monotonosti:
 je rastuća na
je rastuća na
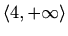 , padajuća na
, padajuća na
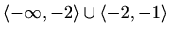
Graf funkcije: slika 5.18
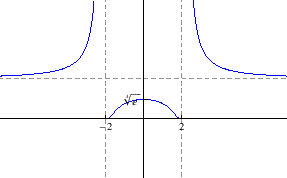
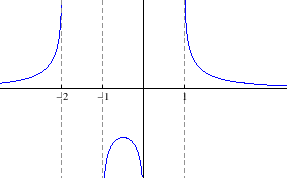
- e)
Područje definicije:
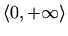
Parnost:
 nije ni parna ni neparna
nije ni parna ni neparna
Nul-točke: nema
Asimptote:
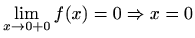 nije vertikalna
asimptota
nije vertikalna
asimptota
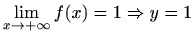 je desna
horizontalna asimptota
je desna
horizontalna asimptota
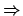 nema kosih asimptota
nema kosih asimptota
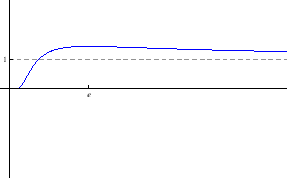
Ekstremi:
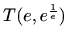 je
lokalni maksimum
je
lokalni maksimum
Intervali monotonosti:
 je rastuća na
je rastuća na
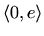 , padajuća na
, padajuća na
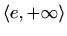
Graf funkcije: slika 5.19
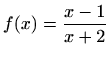 .
.
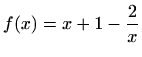 .
.
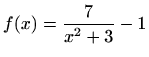 .
.
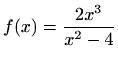 .
.
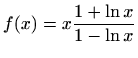 .
.
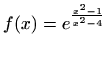 .
.
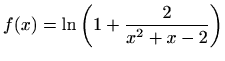 .
.
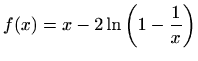 .
.
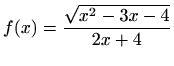 .
.