Deriviranje parametarski zadane funkcije

Jedna od važnih primjena diferencijala je deriviranje parametarski zadanih funkcija. Derivaciju parametarski zadane funkcije

$\displaystyle x=\varphi (t),\quad y=\psi(t), \qquad t\in\mathcal{D}\subseteq \mathbb{R},$

računamo pomoću formule (5.10):

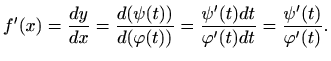
$\displaystyle f'(x)=\frac{dy}{dx}=\frac{d(\psi(t))}{d(\varphi (t))}= \frac{\psi'(t)dt}{\varphi '(t)dt}=\frac{\psi'(t)}{\varphi '(t)}.$

Često se koristi i kraći zapis

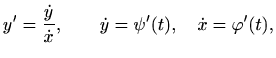
$\displaystyle y'=\frac{\dot y}{\dot x},\qquad \dot y=\psi'(t),\quad \dot x=\varphi '(t),$

pri čemu

označava deriviranje po nezavisnoj varijabli

, a $\dot x$ i $\dot y$ označava deriviranje po parametru.

Primjer 5.10 Odredimo tangentu na krivulju zadanu s

$\displaystyle x=2\cos t, \quad y=\sin t,\qquad t\in[0,2\pi],$

u točki

. Ovo je parametarski zadana elipsa iz poglavlja 5.1.4 koja je prikazana na slici 5.3. Formula (5.10) daje

$\displaystyle y'=\frac{\cos t}{-2\sin t}.$

Odredimo

: iz $x=1=\cos t$ slijedi $\cos t=1/2$ pa je $t=\pi/3$ ili $t=-\pi/3$ . Uvjet

povlači $t=\pi/3$ i $y=\sin \pi/3=\sqrt{3}/2$ . Dakle,

$\displaystyle y'(1)=\frac{\cos \frac{\pi}{3}}{-2\sin \frac{\pi}{3}} =-\frac{\frac{1}{2}}{2 \frac{\sqrt{3}}{2}}=-\frac{1}{2\sqrt{3}}$

pa je jednadžba tražene tangente dana s (5.3).

Formulu za drugu derivaciju parametarski zadane funkcije također dobijemo primjenom formule (5.10):

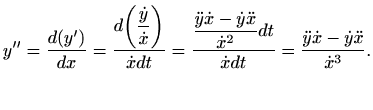
$\displaystyle y''=\frac{d(y')}{dx}= \frac{d\bigg(\displaystyle \frac{\dot y}{\d... ...ddot x}{\dot x^2}dt}{\dot x dt} =\frac{\ddot y\dot x-\dot y\ddot x}{\dot x^3}.$

Ovu formulu smo također mogli izvesti koristeći formulu (5.11).

Više derivacije i diferencijali DERIVACIJE I PRIMJENE Teoremi diferencijalnog računa