☰
matematika1
Sustav nejednadžbi u skupu
OSNOVE MATEMATIKE
Rješenja
Zadaci za vježbu
- 1.
- Riješite sljedeće nejednadžbe:
- a)
-
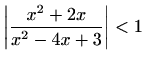 ,
,
- b)
-
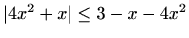 ,
,
- c)
-
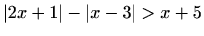 .
.
- 2.
- Dokažite matematičkom indukcijom da za svaki prirodan broj
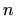 vrijedi
vrijedi
- 3.
- Dokažite matematičkom indukcijom da za svaki prirodan broj
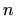 vrijedi
vrijedi
- 4.
- Dokažite matematičkom indukcijom da za svaki prirodan broj
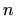 vrijedi
vrijedi
- 5.
- Odredite
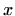 ako je poznato da je treći član u razvoju
binoma
ako je poznato da je treći član u razvoju
binoma
jednak 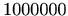 .
.
- 6.
- Odredite onaj član u razvoju binoma
koji se nalazi uz potenciju 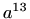 .
.
- 7.
- Izračunajte
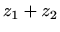 ,
, 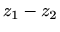 ,
,
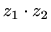 i
i
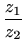 ako je
ako je
- a)
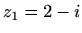 ,
, 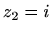 ,
,
- b)
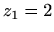 ,
, 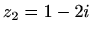 .
.
- 8.
- Odredite realni i imaginarni dio kompleksnog broja
- 9.
- Odredite realan broj t takav da je
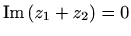 ,
ako je
,
ako je
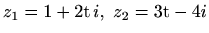 .
.
- 10.
- Riješite jednadžbu
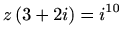 .
.
- 11.
- Odredite sve kompleksne brojeve
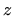 za koje vrijedi
za koje vrijedi
- 12.
- Koristeći trigonometrijski oblik kompleksnog broja
izračunajte:
- a)
-
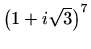 ,
,
- b)
-
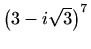 .
.
- 13.
- Koristeći trigonometrijski oblik kompleksnog broja
izračunajte:
- a)
-
![$ \displaystyle \sqrt[4]{-i}$](img440.gif) ;
;
- b)
-
![$ \displaystyle \sqrt[3]{1+i\sqrt{3}}$](img441.gif) .
.
- 14.
- U skupu kompleksnih brojeva riješite jednadžbe:
- a)
-
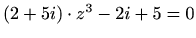 ;
;
- b)
-
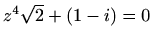 ,
,
- c)
-
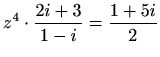 ,
,
- d)
-
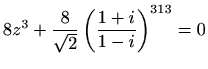 ,
,
- e)
-
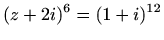 .
.
- 15.
- Odredite i skicirajte skup svih kompleksnih brojeva
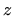 za
koje vrijedi:
za
koje vrijedi:
- a)
-
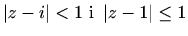 ,
,
- b)
-
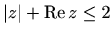 ,
,
- c)
-
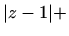 Im
Im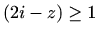 ,
,
- d)
-
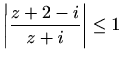 ,
,
- e)
-
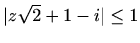 i
i 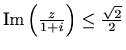 .
.
- 16.
- Odredite sve kompleksne brojeve
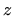 takve da je
takve da je
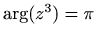 i da su u kompleksnoj ravnini jednako udaljeni od brojeva
i da su u kompleksnoj ravnini jednako udaljeni od brojeva 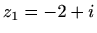 i
i 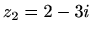 .
.
- 17.
- Odredite sve kompleksne brojeve
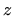 za koje vrijedi
za koje vrijedi
- 18.
- Odredite sve kompleksne brojeve
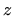 za koje vrijedi
za koje vrijedi
- 19.
- Odredite skup svih kompleksnih brojeva
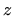 za koje vrijedi
za koje vrijedi
Sustav nejednadžbi u skupu
OSNOVE MATEMATIKE
Rješenja
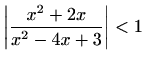 ,
,
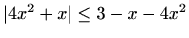 ,
,
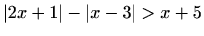 .
.
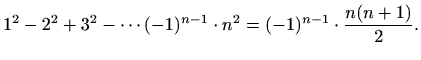
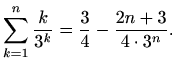
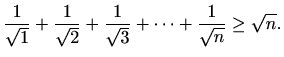
![$\displaystyle \left(\frac{1}{2} \sqrt {a^3} +\sqrt[3]{a^2}\right)^{12}$](img424.gif)
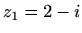 ,
, 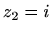 ,
,
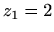 ,
, 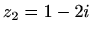 .
.
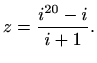
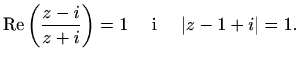
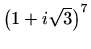 ,
,
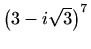 .
.
![$ \displaystyle \sqrt[4]{-i}$](img440.gif) ;
;
![$ \displaystyle \sqrt[3]{1+i\sqrt{3}}$](img441.gif) .
.
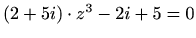 ;
;
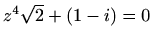 ,
,
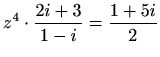 ,
,
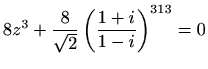 ,
,
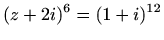 .
.
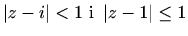 ,
,
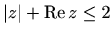 ,
,
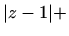 Im
Im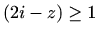 ,
,
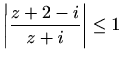 ,
,
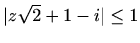 i
i 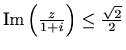 .
.
![$\displaystyle \arg\left[z^3\left(\frac{1}{2}-\frac{\sqrt{3}}{2}i\right)\right]=\frac{5\pi}{3} \quad\textrm{ i }\quad {\vert z\vert}^2+\vert z\vert-12=0.$](img458.gif)
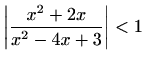 ,
,
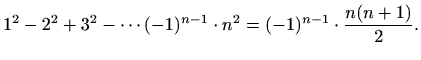
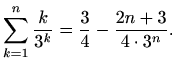
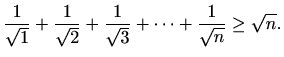
![$\displaystyle \left(\frac{1}{2} \sqrt {a^3} +\sqrt[3]{a^2}\right)^{12}$](img424.gif)
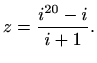
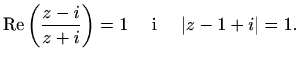
![$ \displaystyle \sqrt[3]{1+i\sqrt{3}}$](img441.gif) .
.
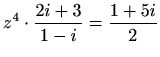 ,
,
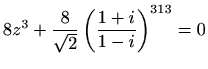 ,
,
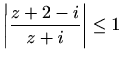 ,
,
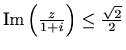 .
.
![$\displaystyle \arg\left[z^3\left(\frac{1}{2}-\frac{\sqrt{3}}{2}i\right)\right]=\frac{5\pi}{3} \quad\textrm{ i }\quad {\vert z\vert}^2+\vert z\vert-12=0.$](img458.gif)