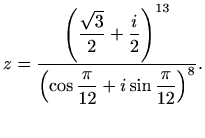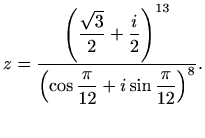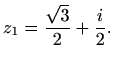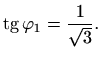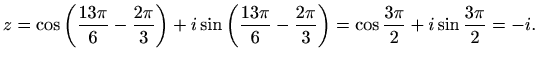Dijeljenje kompleksnih brojeva

Odredite kompleksni broj

$\displaystyle z=\frac{\displaystyle \left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^{13}}{\displaystyle\left(\cos\frac{\pi}{12}+i\sin\frac{\pi}{12}\right)^8}.$

Rješenje. Odredimo prvo trigonometrijski oblik kompleksnog broja

$\displaystyle z_1=\frac{\sqrt{3}}{2}+\frac{i}{2}.$

Prema

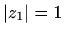[M1, poglavlje 1.8.1] je $\vert z_1\vert=1$ , a za argument 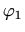$\varphi _1$ vrijedi

$\displaystyle \mathop{\mathrm{tg}}\nolimits \varphi _1=\frac{1}{\sqrt{3}}.$

Budući je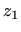

iz prvog kvadranta, njegov trigonometrijski oblik glasi

$\displaystyle z_1=\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}.$

De Moivreova formula [M1, (1.4)]

daje

$\displaystyle z=\frac{\displaystyle \left(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\... ...}+i\sin\frac{13 \pi}{6}}{\displaystyle\cos\frac{2 \pi}{3}+i\sin\frac{2 \pi}{3}}$

pa iz formule

za dijeljenje kompleksnih brojeva u trigonometrijskom obliku slijedi

$\displaystyle z=\cos\left(\frac{13\pi}{6}-\frac{2\pi}{3}\right)+i\sin\left(\frac{13\pi}{6}-\frac{2\pi}{3}\right) =\cos\frac{3 \pi}{2}+i\sin\frac{3 \pi}{2}=-i.$