Konvergentan red funkcija može se, uz određene
uvjete, derivirati član po član (vidi M1, poglavlje 6.4.3)
![]() .
Slična
je situacija i s integriranjem. Najvažnija primjena integriranja reda
funkcija je računanje integrala funkcija koje nisu elementarno
integrabilne. Druga primjena je razvijanje u red potencija onih
funkcija kod kojih se to ne može direktno napraviti pomoću
Taylorove formule (vidi
.
Slična
je situacija i s integriranjem. Najvažnija primjena integriranja reda
funkcija je računanje integrala funkcija koje nisu elementarno
integrabilne. Druga primjena je razvijanje u red potencija onih
funkcija kod kojih se to ne može direktno napraviti pomoću
Taylorove formule (vidi
![]() M1, poglavlje 6.5).
M1, poglavlje 6.5).
U sljedećem teoremu koriste se pojmovi uniformne
konvergencije
reda
funkcija (vidi
![]() M1, poglavlje 6.4) i reda
potencija (vidi
M1, poglavlje 6.4) i reda
potencija (vidi
![]() M1, poglavlje 6.4.2).
M1, poglavlje 6.4.2).
Pokažimo kako pomoću teorema 1.9 možemo izračunati razvoj u red potencija integrala koji nisu elementarno rješivi.
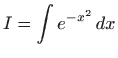
nije elementarno rješiv, odnosno rješenje nije elementarna funkcija i ne može se prikazati konačnim brojem zbrajanja, oduzimanja, množenja, dijeljenja i komponiranja elementarnih funkcija. Ovaj integral je od velike važnosti u teoriji vjerojatnosti i statistici jer funkcija vjerojatnosti Gaussove ili normalne razdiobe ima oblik funkcije
Maclaurinov razvoj
funkcije ![]() glasi (vidi
glasi (vidi
![]() M1, poglavlje 6.5)
M1, poglavlje 6.5)
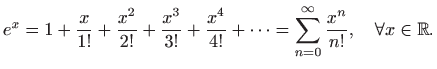
Pri tome je konvergencija uniformna (vidi
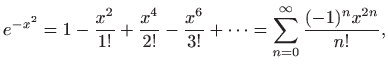
pri čemu je konvergencija uniformna. Teorem 1.9 daje
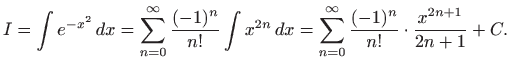
Dakle, našli smo razvoj traženog integrala u uniformno konvergentan red potencija. Pomoću ovog reda možemo izračunati vrijednost funkcije
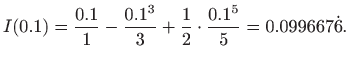
Četvrti član reda (za
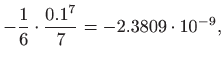
pa zaključujemo da pogreška nije veća od
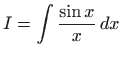
također nije elementarno rješiv. Maclaurinov razvoj funkcije
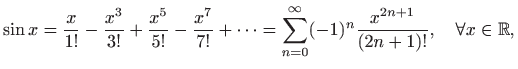
pri čemu je konvergencija uniformna. Za
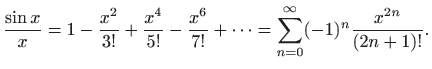
Primijetimo da je red na desnoj strani definiran za svaki
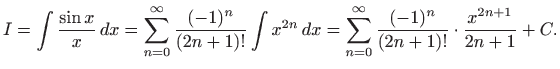
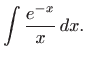
Octave On-line[Octave On-line Home] [Octave User's Guide] |
x=-4:0.01:4; plot(x,exp(-x.^2))Nacrtajte funkciju na različitim intervalima koristeći program Octave On-line.
Teorem 1.9 također možemo iskoristiti za računanje razvoja u red potencija onih funkcija kod kojih to ne možemo direktno napraviti.
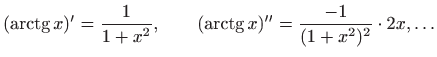
pa derivacije postaju vrlo složene. Zato ćemo koristiti geometrijski red (vidi
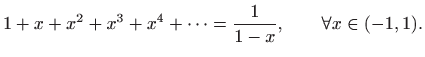
Zamijenimo li
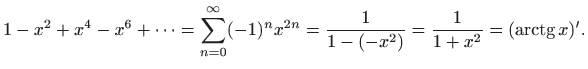
Teorem 1.9 daje
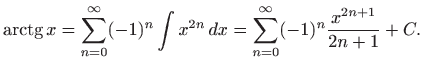
Na lijevoj strani jednakosti nalazi se konkretna funkcija pa konstanta
Ispitajmo konvergenciju reda na desnoj strani u rubovima intervala.
U točki ![]() red glasi
red glasi
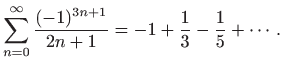
Ovaj red konvergira po Leibnitzovom kriteriju (vidi
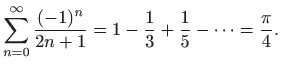
Gornji red možemo koristiti za računanje broja ![]() , međutim
konvergencija je vrlo spora. Naime, red je alterniran pa
zaključujemo da apsolutna vrijednost pogreške prilikom aproksimacije konačnom parcijalnom
sumom nije veća od apsolutne vrijednosti prvog zanemarenog člana (slično smo već zaključili
u primjeru 1.14a). Na primjer, kada zbrojimo prvih
, međutim
konvergencija je vrlo spora. Naime, red je alterniran pa
zaključujemo da apsolutna vrijednost pogreške prilikom aproksimacije konačnom parcijalnom
sumom nije veća od apsolutne vrijednosti prvog zanemarenog člana (slično smo već zaključili
u primjeru 1.14a). Na primjer, kada zbrojimo prvih ![]() članova reda, apsolutna vrijednost pogreške je manja od
članova reda, apsolutna vrijednost pogreške je manja od
![]() , što znači da smo
izračunali tek prve tri decimale broja
, što znači da smo
izračunali tek prve tri decimale broja ![]() .
.
Octave On-line[Octave On-line Home] [Octave User's Guide] |