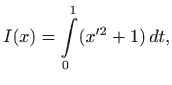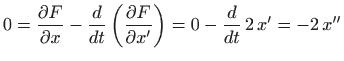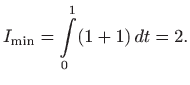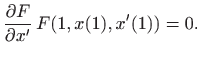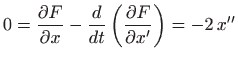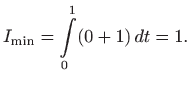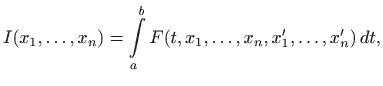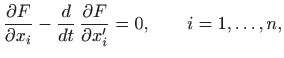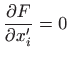Primjer 4.23 Riješimo
problem najmanjeg oplošja:
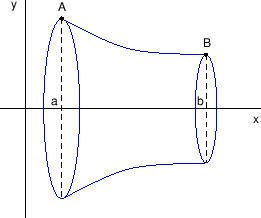
od svih krivulja koje prolaze točkama
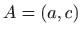
i
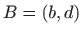
nađimo onu koja
rotacijom oko
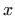
-osi opisuje tijelo najmanjeg oplošja (slika
4.19).
Slika:
Problem najmanjeg oplošja
 |
Prema poglavlju 2.6.4, oplošje rotacijskog tijela računa se formulom
pri čemu je
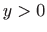
. Dakle, potrebno je minimizirati funkcional
Euler-Lagrangeova jednadžba glasi
| 0 |
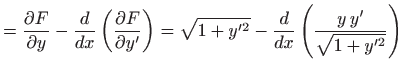 |
|
| |
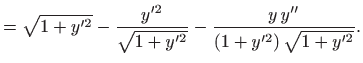 |
|
Množenjem jednadžbe s
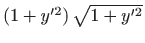
dobili smo
diferencijalnu jednadžbu drugog reda:
Jednadžbu ćemo riješiti koristeći supstituciju
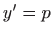
.
Kako je
gornja diferencijalna jednadžba prelazi u jednadžbu sa separiranim varijablama
odnosno
Integriranje daje
za neku konstantu
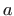
. Odavde slijedi
odnosno
Integriranje daje (vidi poglavlje
1.1.1)
za neku konstantu b pa je konačno
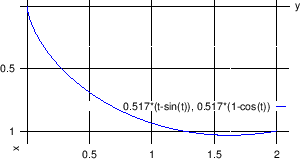
Dakle, rješenje je lančanica
(vidi
![[*]](../icons.gif/crossref.gif)
M1,
poglavlje 4.6.9). Provjera dovoljnih uvjeta ekstrema daje
pa se zaista radi o minimumu.
Konstante
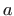
i
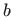
se određuju iz početnih uvjeta i ne mogu se
odrediti analitički.
Međutim, program za određivanje početnih uvjeta može se jednostavno
programirati u programskom jeziku
Matlab
.
Za rubne uvjete 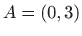 i
i 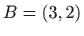 program koji računa konstante
program koji računa konstante 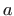 i
i 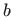 i
potom crta rješenje glasi:
i
potom crta rješenje glasi:
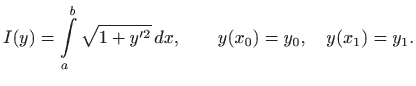
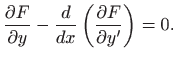
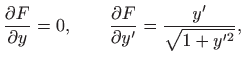
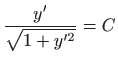
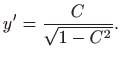
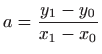
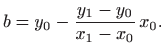
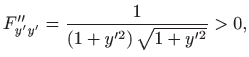
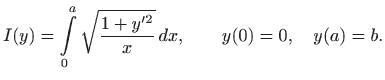
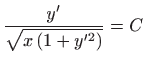
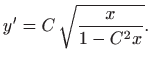
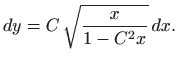
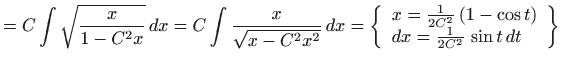
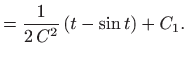
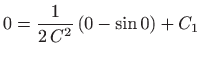
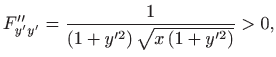
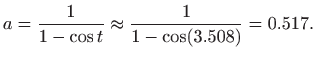

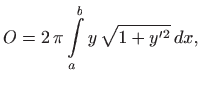
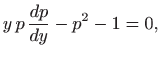
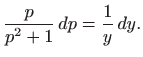
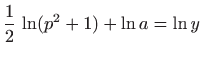
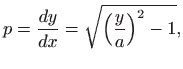
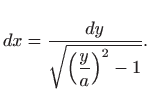
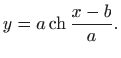
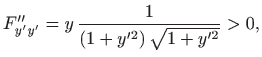
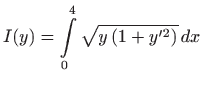 ,
,
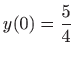 ,
,
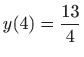 .
.
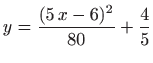 .
.
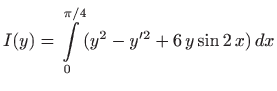 ,
,