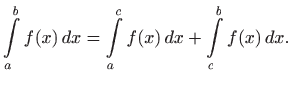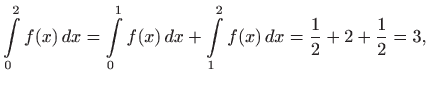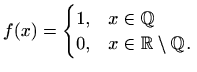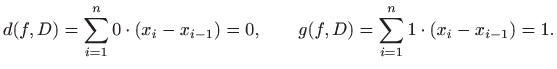Skup svih dekompozicija segmenta
Neka je
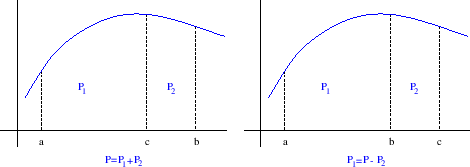
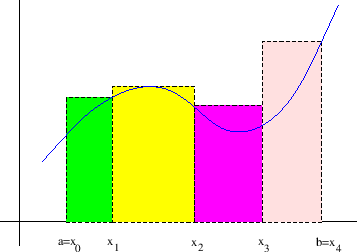
![]() omeđena funkcija. Gornja integralna suma je broj (slika 2.1)
omeđena funkcija. Gornja integralna suma je broj (slika 2.1)
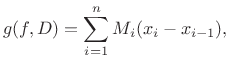
gdje je
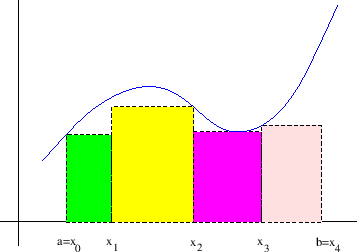
Donja integralna suma je broj (slika 2.2)
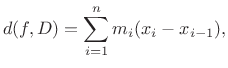
gdje je
Gornji (Riemannov) integral je broj
a donji (Riemannov) integral je broj
Brojevi
Ako je ![]() , onda kažemo da je funkcija
, onda kažemo da je funkcija ![]() (Riemann) integrabilna na segmentu
(Riemann) integrabilna na segmentu
![]() .
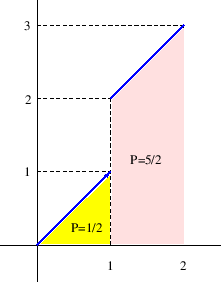
Riemannov integral
ili određeni integral
funkcije
.
Riemannov integral
ili određeni integral
funkcije ![]() od
od ![]() do
do ![]() je broj
je broj
Određeni integral označavamo s
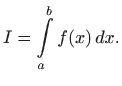
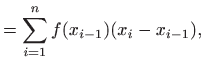
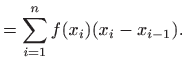
 .
.
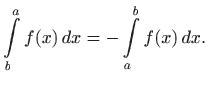
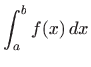 varijabla
varijabla