Izračunajte volumen tijela omeđenog površinama
![]() ,
,
![]() i ravninom
i ravninom ![]() .
.
Rješenje.
Volumen tijela ![]() omeđenog plohama
omeđenog plohama ![]() i
i ![]() iznad područja
iznad područja ![]() ,
pri čemu je
,
pri čemu je
![]() ,
,
![]() , prema
, prema
![]() [M2, poglavlje 4.2.1], računa se po formuli
[M2, poglavlje 4.2.1], računa se po formuli
![$\displaystyle \displaystyle V(\Omega) = \iint\limits_D \left[f(x,y)-g(x,y)\right] dx dy$](img1310.gif) . . |
Uvedimo polarne koordinate
Jednadžba kružnice ![]() u novim koordinatama glasi
u novim koordinatama glasi ![]() ,
a jednadžba kružnice
,
a jednadžba kružnice ![]() glasi
glasi ![]() .
.
Volumen tijela omeđenog širim paraboloidom ![]() i ravninom
i ravninom ![]() jednak je
jednak je
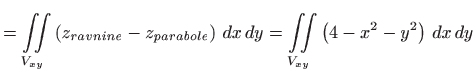 |
||
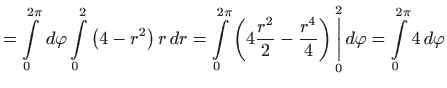 |
||
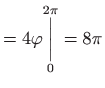 , , |
a volumen tijela omeđenog užim paraboloidom
![]() i ravninom
i ravninom ![]() jednak je
jednak je
![$\displaystyle =\iint\limits_{V_{xy}}\left[ 4-2\left( x^{2}+y^{2}\right) \right]
dx dy$](img1321.gif) |
||
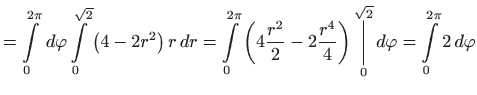 |
||
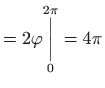 , , |