Rekurzivna formula je formula kojom se izraz ovisan o nekom parametru izražava pomoću izraza istog oblika ovisnog o istoj ili nekoj drugoj vrijednosti tog parametra.1.3 Formalna definicija je sljedeća: neka za niz funkcija
postoje neodređeni integrali
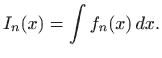
Formula oblika
zove se rekurzivna formula za niz integrala
Primjenu rekurzivnih formula za nalaženje integrala ilustrirat ćemo na sljedećem važnom primjeru koji je sastavni dio integriranja racionalnih funkcija u poglavlju 1.4. Nađimo
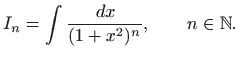
Za
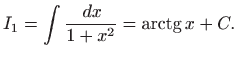
Za
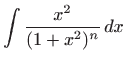 |
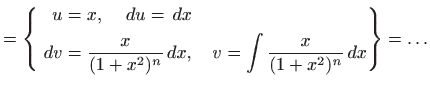 |
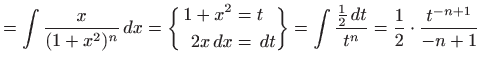 |
||
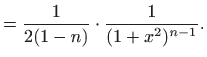 |
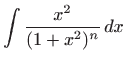 |
 |
|
 |
 |
||
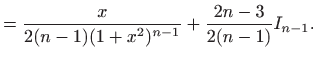 |
Uzastopnom primjenom ove formule lako nađemo integral ![]() za bilo
koji
za bilo
koji ![]() . Na primjer, za
. Na primjer, za ![]() imamo
imamo
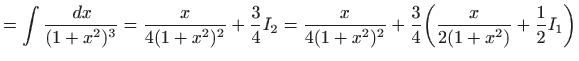 |
||
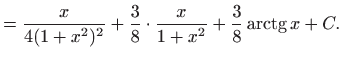 |