☰
matematika2
Sferne koordinate u trostrukom
VIŠESTRUKI INTEGRALI
Koordinate težišta homogenog tijela
Volumen tijela
Izračunajte uz pomoć trostrukog integrala volumen tijela omeđenog plohama
- a)
-
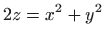 i
i
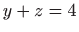 ,
,
- b)
-
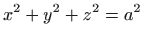 i
i
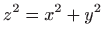 izvan stošca.
izvan stošca.
Rješenje.
- a)
- Tijelo omeđeno paraboloidom
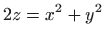 i ravninom
i ravninom
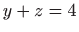 prikazano je na slici 4.14.
prikazano je na slici 4.14.
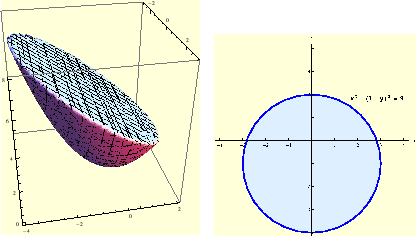
Slika:
Tijelo omeđeno paraboloidom
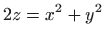 i ravninom
i ravninom
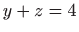 , i njegova projekcija na
, i njegova projekcija na 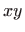 ravninu.
ravninu.
 |
Odredimo projekciju tijela na 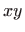 ravninu.
Iz
ravninu.
Iz
izjednačavanjem 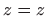 dobijemo
dobijemo
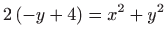 , , |
|
odnosno
Ovo je jednadžba kružnice polumjera 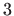 sa središtem
sa središtem
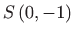 . Uvedimo
pomaknute cilindrične koordinate:
. Uvedimo
pomaknute cilindrične koordinate:
Vrijedi 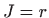 ,
,
![$ \varphi \in \left[ 0,2\pi \right] $](img1400.gif) ,
,
![$ r\in \left[ 0,3\right] $](img1401.gif) i
i
Volumen je jednak
- b)
- Tijelo omeđeno zadanim
stošcem i sferom za
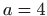 je prikazano na slici 4.15.
je prikazano na slici 4.15.
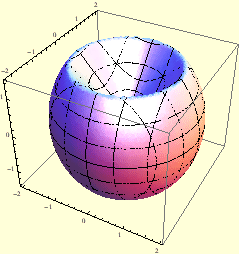
Slika:
Tijelo omeđeno sferom
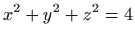 i stošcem
i stošcem
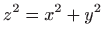 (izvan stošca).
(izvan stošca).
 |
Uvedimo sferne koordinate
Vrijedi
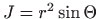 ,
,
![$ \varphi \in \left[ 0,2\pi \right] $](img1400.gif) , i
, i
![$ r\in
\left[ 0,a\right] $](img1415.gif) . Presjek stošca
. Presjek stošca
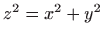 i ravnine
i ravnine 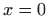 (
(
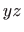 koordinatne ravnine) čine pravci
koordinatne ravnine) čine pravci 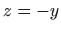 i
i 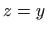 , pa je
, pa je
![$ \Theta \in
\left[ \frac{\pi }{4},\frac{3\pi }{4}\right] $](img1419.gif) .
Volumen je
.
Volumen je
Sferne koordinate u trostrukom
VIŠESTRUKI INTEGRALI
Koordinate težišta homogenog tijela
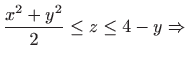
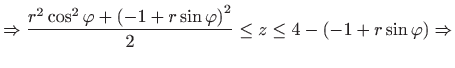
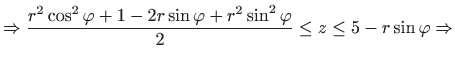
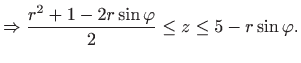
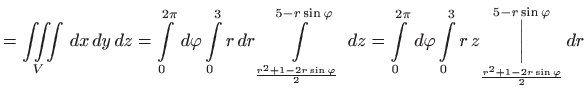
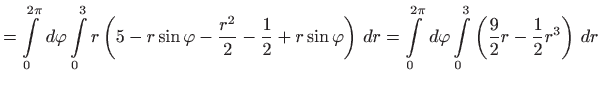
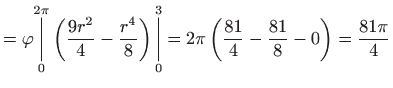 .
.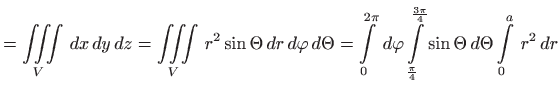
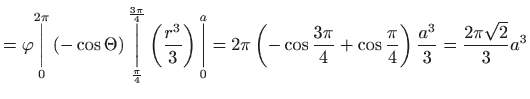 .
.